JWST ETC Residual Flat Field Errors

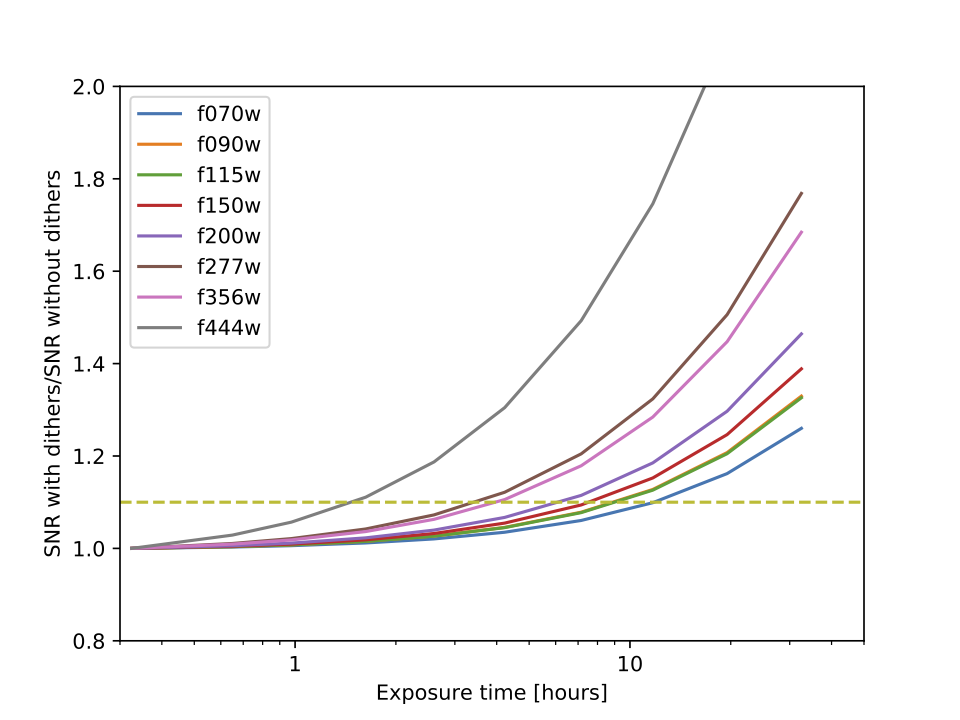
The JWST ETC includes pixel-to-pixel noise due to an imperfectly corrected flat field. This noise source is often mitigated by dithering.

Since the ETC currently does not model dithers, except in a limited sense for a few special cases, such as coronagraphy and IFU spectroscopy, the absence of dithers will limit the sensitivity for very deep (>10,000 s) imaging observations and will also limit the signal-to-noise ratio (SNR) that can be achieved for bright sources. 

On this page


Users should be aware that the issues presented in this article were fixed in the ETC 1.2.2 release. Specifically, the Total Dithers quantity on the Detector Setup tab will decrease the residual flat field error by \sqrt{n_{\rm dither}}. Conversely, multiple integrations will not decrease the residual flat field error. In this way it is possible to investigate the effect of dithering on the predicted SNR.

Words in bold are GUI menus/
panels or data software packages; 
bold italics are buttons in GUI
tools or package parameters.

In its error model, the ETC includes an error term that models residual flat field errors. For a typical observation, each exposure will be divided by a pixel flat field, which is intended to normalize the relative response (quantum efficiency) of each pixel. However, the flat field is an imperfect measurement itself, and consequently, there will always be some residual pixel-to-pixel response variation, even after division by the flat field. In the absence of dithers, where the pointing of the telescope is the same for multiple exposures, the light from a source will occupy the same pixels on the detector for each exposure. In this case, the presence of a residual flat field error may eventually limit the depth of an observation. JWST detectors are required to have flat fields with pixel-to-pixel variations <10%. In the ETC, the residual flat field error, after flat field correction, is typically assumed to be in the range of 0.1 to 1.0%. Currently, the ETC only models dithers in a very limited sense, and may, therefore, underestimate the sensitivity of very deep observations.

Effects of the residual flat field error on deep observations

As a general rule, observers dependent on total exposure times in excess of ~10,000 seconds for broadband imaging (and somewhat longer for most spectroscopy modes) should be aware of the effects of residual flat field errors. In the limit of extremely long total exposure times, in the absence of dithers, all observations will eventually be limited by the residual flat field error. The practical effect is that ETC calculations will have a "noise floor," beyond which observations with increasing numbers of exposures no longer increase the signal-to-noise ratio by \sqrt{n_{\rm dither}}. This is true both for faint and bright sources. Furthermore, in the case of faint sources, background limited observations (i.e., with high background levels compared to the source) are particularly susceptible to residual flat field errors. This means that narrowband filters will take longer to be limited by the flat field error, and spectroscopy is similarly less affected.

Figure 1. Relative effect of dithering in decreasing residual flat field error as a function of total exposure time for NIRCam imaging

The relative effect of dithering decreasing the residual flat field error for NIRCam imaging as a function of total exposure time. This calculation assumes ~1,000 s exposures. Departures above 10% (dashed line) indicates that the non-dithered ETC sensitivities may be conservative if significant numbers of dithers are used.

Effects of the residual flat field error on observations of bright sources

Another effect of the residual flat field error is that there is a limit on how high the SNR will get for bright sources. The SNR ceiling will depend on the flat field error assumed for each instrument, as well as the number of pixels the signal is spread over. For most modes, observations of point sources will be limited to SNRs of a few 100. Note that time-series observations (e.g., of exoplanet transits) are immune to this, as they rely on relative measurements on the same pixels.


The special case of NIRSpec MSA 

Observers using the multi-shutter array (MSA) with NIRSpec should be aware that the residual flat field error is significantly worse than for other modes, as the flat fields for the many individual shutters are necessarily of lower quality than what can be done by, e.g., imaging. In this case, it is not expected that the noise floor can be improved using the above method, and it is recommended that the ETC Total Dithers parameter is used to predict NIRSpec MSA performance also for long total exposure times. 



Notable updates
  •  
    Warning added to reflect changes in the ETC 1.2.2 patch release in regards to the residual flat field error.
Originally published