NIRSpec's multipurpose design necessitates a complex optical path with several particular and peculiar features that must be accounted for in the calibration scheme. This article provides background information about the NIRSpec calibration concept, with emphasis on methods used to overcome peculiarities introduced by the micro shutter assembly (MSA). 

See also: Stages of JWST Data Processing
ReadTheDocs documentation: Introduction to the JWST Pipeline, Reference File information, Reference File Types

In the sections that follow, an overview is presented on the distinctive features of NIRSpec data and the novel calibration methodology built into the pipeline to handle those idiosyncrasies. This content is intended to be useful for understanding and contextualizing the mode-specific calibration status articles listed below:

• NIRSpec IFU Calibration Status
• NIRSpec Fixed Slit Calibration Status
• NIRSpec MOS Calibration Status
• NIRSpec BOTS Calibration Status

This article is not intended to address instrument-independent calibrations and conceptually straightforward topics such as ramp-to-slopes calibration dark subtraction, bias and linearity corrections, or cosmic ray and snowball mitigation (much of which can be found in the article calwebb_detector1 on stage 1 of JWST data processing). This article does not provide details of current or ongoing calibration analysis and uncertainty, but that information can be found in the articles for NISpec modes BOTS, FS, IFU and MOS.

---

Geometric characterization

NIRSpec calibration is powered by a parametric model of the instrument, describing the internal light path, and precisely constrained using a specially designed set of calibration observations. The current status of the instrument model calibration can be found at NIRSpec Instrument Model Calibration Status.

Pixel-by-pixel wavelength computation

ReadTheDocs documentation: Assign WCS, Extract 2D Spectra

The wavelength of the light incident on each detector pixel depends on the instrument mode, the aperture through which the target is viewed, and the selected disperser. A fourth variable is introduced by the small “GWA-tilt” (grating wheel assembly tilt) effect, a wavelength shift due to the offset in the resting location of the grating wheel assembly after each move, which is well calibrated from the output voltage of a magnet-based tilt sensor. The use of the parametric model is vital, as it is not feasible to calibrate individually by observing the spectrum from every one of the 250,000 shutters for every mode, disperser, and possible GWA tilt.

For a source observed with a given instrument configuration, the model uniquely identifies the spatial and spectral coordinates of the source light incident on each pixel of the detectors. The in-flight calibration of the instrument model derived from commissioning data yields residuals of 0.05–0.1 pixel RMS (depending on the disperser), which should be compared to the maximum acceptable standard deviation of 1/10 of a resolution element (0.2 pixels), as stated in the instrument calibration error budget. The full instrument model fit, including the GWA-tilt sensor correction, will be monitored and updated as needed throughout nominal operations.

All subsequent steps in the calibration rely on each pixel being associated with an incident wavelength.

This calibration is generated during the Assign WCS step (assignwcs in calwebb_spec2) using the NIRSpec instrument model (reference files "FPA," "CAMERA," "DISPERSER," "COLLIMATOR," "MSA," "WAVELENGTHRANGE," "FORE," "OTE," "IFUFORE," "IFUSLICER," "IFUPOST" in CRDS), and is applied during the Extract 2D step (extract2d in calwebb_spec2) which again uses the "WAVELENGTHRANGE" reference file in CRDS together with the previously generated WCS solution.

Wavelength correction for off-center sources

ReadTheDocs documentation: Wavelength Correction.

The wavelength solution from the parametric model assumes that the source is centered in the aperture, and therefore it must be corrected via a dedicated reference file. This correction is only relevant for the fixed slit and MOS modes, and is only applied automatically by the pipeline for point sources.

Note that the effects of diffraction on the PSF imply that the required correction is not a bulk shift, but a function of wavelength, and as such, simply running the instrument model (which is purely geometric and not radiometric) assuming a different source position does not solve the problem.

This correction is applied during the Wavelength Correction step (WavecorrStep in calwebb_spec2) using the "WAVECORR" reference file in CRDS.

---

Radiometric corrections

The radiometric calibration in the NIRSpec pipeline depends on the source type, with 2 separate branches:

• Point source: Based on observations of spectrophotometric standard point sources through the center of a fiducial aperture, this calibration will account for off-center locations (which affects the wavelength solution) as well as slit losses, and results in a 1-D product in flux units.
• Uniform illumination: For extended sources, the uniform case should be applied, which will result in products in units of surface brightness. Note that any non-uniformity in the source can produce uncertainties in the results.

Flat fielding

ReadTheDocs documentation: Flat Reference Files for NIRSpec Spectroscopy

For NIRSpec, flat fielding is used as a broad term, encompassing corrections for the total throughput losses along the entire optical path, from the observatory primary mirror to the instrument detector subsystem, accounting for variations as a function of both wavelength and field angle (i.e., source position within the field of view). This includes the multiplicative combination of effects due to all reflective surfaces, transmission filters, and dispersers, and it is also convenient to consider the detector response as a component of the total “throughput losses,” so detector effects are also folded into the flat field.

The spectroscopic flat field correction is challenging, as each disperser introduces a different wavelength dependence to the instrument throughput. In the case of the MOS mode, this is further complicated as each detector pixel can be illuminated by many different wavelengths, depending on the location of the utilized aperture(s) within the field of view. For the fixed slit and IFU modes, for a given disperser, the same wavelength will always fall on the same pixel, once the GWA-tilt and off-center source effects have been corrected.

The NIRSpec flat field is separated into 3 manageable components, each with a dedicated set of reference files. This concept was strongly driven by 3 constraints: (1) the inability to measure the fore-optics throughput during ground testing, as “on-sky” observations of a flat lamp were not feasible, (2) light from the internal calibration assembly of NIRSpec does not pass through the instrument fore-optics, entering the optical path after the filter wheel assembly (FWA), and (3) due to shadowing by the MSA structure, the detector response could never be measured as thoroughly or completely as it was in the laboratory before integration into NIRSpec.

• The D-flat encapsulates both the wavelength-dependent quantum efficiency of each pixel, measured over the full operational spectral range of the detectors, as well as the high spectral resolution behavior of the anti-reflection coating.
• The F-flat includes the relative throughput losses of all reflections along the JWST optical telescope element and the NIRSpec fore-optics as well as the transmission curve of the selected filter in the FWA. These losses vary with both wavelength (due to the reflectivity curves of the various mirrors) and field angle (as not all mirrors are fully illuminated by the beam). The F-flat can only be measured on-sky, and, in practice, is derived from extracted 1-D spectra of spectrophotometric calibration sources observed at many positions in the instrument field of view.
• The S-flat corresponds to the optical path starting from the aperture plane where the optical paths for different modes diverge rapidly as the light passes through apertures of varying widths and locations, and hits downstream optical elements at different angles. After passing the selected disperser mounted on the GWA, wavelengths are separated, taking somewhat different optical paths through the camera optics before falling on the detector.

The S-flat corrections are determined via exposures of the internal calibration flat lamps. For the fixed slit and IFU modes, for a given instrument configuration (filter and grating), the incident light on any given pixel will always have the same wavelength, so many flat field calibration exposures can be combined to increase signal-to-noise ratio and hence derive an accurate master S–flat. The GWA-tilt effect is assumed to be weak enough to be ignored for S-flat generation, demonstrated by a lack of significant difference after exposures with outlying tilt readings are removed from the processing.

For the MOS mode, correspondence between wavelength and pixel also depends on which microshutters are open. The need to maximize telescope efficiency dictates that a dedicated flat field observation per configuration is impractical, and there are too many possibilities for all shutters to be covered by a complete set of calibration exposures. Consequently, it has not been feasible to generate an “observed” MOS S-flat with high enough signal-to-noise ratio. The current S-flat reference files provide no large-scale spatial variation but do encapsulate the fast wavelength variations. Note that when combined with the other flat field components, pixel-to-pixel variation is covered by the D-flat (ensuring sufficient calibration of the pixels in a given trace when collapsing to 1-D), and larger scale variation should be probed by the F-flat (allowing for a combination of multiple nodding locations).

The correction for all these effects could require very large reference files. For the D- and S-flats, the flat field per detector would require a cube 2048 × 2048 × nλ, where nλ probes the full NIRSpec wavelength range with a sampling at least as good as the instrument resolution. The F-flat provides spatial information per slit, slice, or shutter, depending on the instrument mode, although this still would require a cube (2 ×171) × (2 × 365) × nλ for MOS.

However, smaller reference files can be generated, resulting in more practical computational performance, because small-scale “fast” spectral variations can be separated into a single vector component. The remaining pixel-to-pixel (spatially-dependent) variation is then assumed to have only a “slow” dependence on wavelength, and can be encapsulated in a cube with a sparse spectral sampling. For example, in the D–flat, the vector component traces the (spatially universal) “fast” wavelength dependence of the anti-reflection coating, and our assumption of “slow” wavelength variation in the residual pixel-to-pixel component is confirmed empirically from test data. For the F- and S-flats, the assumption that there are no small-scale spatial variations appears safe, as for typical sources, the size of interest is small compared to the mirror size and hence differential reflectivity along the optical path should be minimal. Hence, the 2048 × 2048 × nλ cube is dramatically reduced in size to a 1 × nλ vector and a 2048 × 2048 × cλ cube where the coarse sampling cλ ≪ nλ.

In brief, the pipeline builds the master flat field for a given exposure on the fly, using knowledge of the instrument configuration (mode, aperture, filter, grating) and incident wavelength illuminating each pixel (via the instrument model) in order to interpolate the appropriate value in the fast vector and coarsely-sampled cube for each of the D-, S- and F-flats. The master flat field is the combination: D_vector × D_cube × S_vector × S_cube × F_vector × F_cube. Note that the D- and S-flat cubes provide spatial information per physical pixel, so there is a version for each NIRSpec detector (as well as per mode, grating, and filter), while the F-flat is detector-agnostic.

This calibration is applied during the Flatfield Correction step (flat_field in calwebb_spec2) using the "FFLAT," "SFLAT," and "DFLAT" reference files in CRDS. For NIRSpec, the actual flux calibration conversion is done in the flat_field step using the F-flat fast variation vector which contains the conversion from DN/s to MJy. After the flat_field step, all 2-D spectral data are in units of MJy/pixel.

Path loss correction

ReadTheDocs documentation: Path loss correction.

The path loss of light going through the NIRSpec spectrograph is caused mainly by geometric and diffraction losses. Additionally, for uniform-type sources observed through the microshutters, although the geometric losses are not relevant, the presence of the microshutter bars will also result in flux losses.

• Geometric losses (also known as slit losses): This occurs when the reduced size of the aperture restricts the incoming flux collected from a target by the telescope. In NIRSpec, at longer wavelengths, geometric losses increase as a result of the broadening of the PSF due to diffraction (OTE and NIRSpec’s fore-optics). The effect of geometric losses for NIRSpec fixed slit and MOS observations depends on the source location within the aperture. For data taken with the IFU, geometric losses can be ignored since the light falling outside a slice is not lost but collected by the neighboring slices.
  
  
• Diffraction losses: The truncation that takes place in the image plane (fixed slit and microshutter apertures, or slicer for the IFU) causes a widening of the illumination to the extent that the beam is larger than the surface of the disperser in the GWA, resulting in a partial loss of light. The path loss correction addresses both diffraction and geometric losses together, since quite often it is not possible to disentangle them, especially when using on-sky observations. The correction depends on several parameters: aperture width; the type of object (point source or extended); for point sources, their position within the aperture; and wavelength.

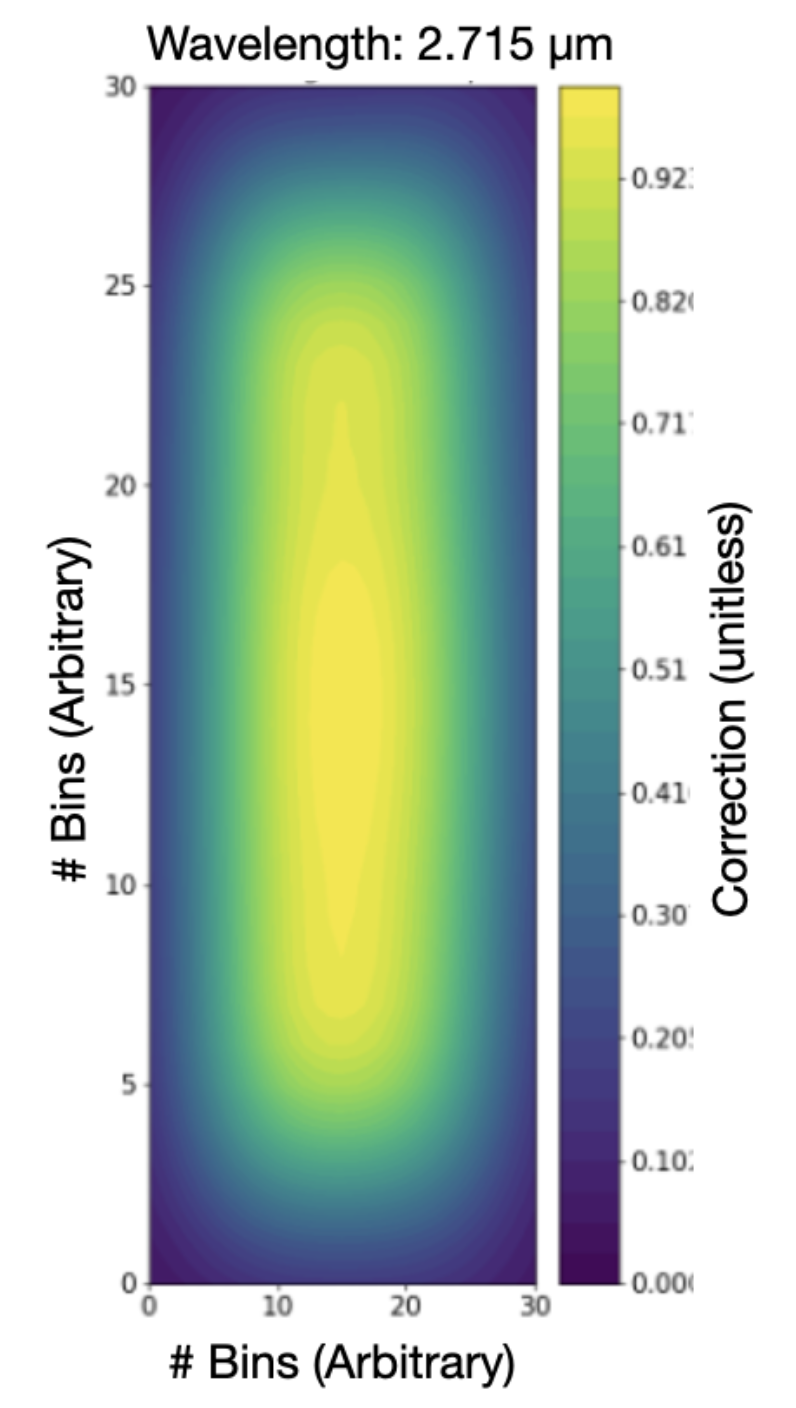
The path loss correction for point sources is normalized to 1.0 in the center of the slit, and it is smaller than 1.0 for off-center sources. This definition ensures self-consistency with the flux calibration, which incorporates the effects of geometric and diffraction losses. In other words, it is assumed that a source centered in the slit has no path losses. For uniform sources, it includes the correction required to go from a centered point source, which is the reference of NIRSpec’s radiometric calibration, to a uniform illumination source. The current model assumes a fully non-coherent illumination with no diffraction effects, resulting in the correction for a uniform source corresponding to the inverse of the path loss correction for a centered source. The path loss correction is also wavelength-dependent, increasing towards longer wavelengths. The path loss reference file is, therefore, a cube that provides the slit losses across any given fixed slit or MOS microshutter at 21 discrete wavelengths ranging from 0.6 to 5.3 µm. Figure 3 includes an example of how the path losses look like for MOS at  2.7 µm.

Further information on how the path loss is derived from a model and observational point of view is provided in Alves de Oliveira et al. (2018) and in this technical document.

The path loss correction is applied for point sources during the Path loss Correction step (pathloss in calwebb_spec2) using the "PATHLOSS" reference file in CRDS. 

Barshadow correction

ReadTheDocs documentation: Barshadow Correction

When using NIRSpec in MOS mode, adjacent microshutters are opened to emulate a slitlet, which is, however, not continuous but interrupted by the presence of bars between the shutters. These bars will mask part of the sources, whether they are point or uniformly extended sources such as the sky background, and this effect needs to be calibrated. For point sources, no attempt is made to correct for the impact of the bars on the spatial profile of the source on the detectors but, by the design of NIRSpec’s radiometric calibration scheme, the associated loss of light is accounted for in the path loss correction so that when collapsing the data along the spatial direction, the resulting 1-D spectrum is correctly calibrated. 

For uniform sources, the spatial profile of the sources is also corrected in a special step called the MSA barshadow correction. Assuming uniform illumination, there are 2 ways in which the bars affect the flux for a given pixel. On the one hand, the size of the projection of the shadow of the bars will vary with wavelength since it is the convolution of the shape of the bars by the PSF of the spectrograph. On the other hand, there is an aliasing effect which is a function of how the sampling is performed. The fact that the spectra are not aligned with the detector rows and columns translates into a rapid evolution of the aliasing effect. A correction is, therefore, dependent on the profile of the optical image of the bars along the spatial direction on the detectors, any cross talk between neighboring pixels, and the actual sampling of the image of the bar by a given pixel.

In particular, this correction must be applied to each individual background spectrum before being combined into a master background. Alternately, if the correction is not applied, then only fully unshadowed pixels should be used in producing the 1-D background spectra (there are typically 2–3 such pixels in the cross-dispersion axis from each shutter).

The values for the barshadow reference file vary from 1.0 at the un-illuminated areas to 0.4–0.5 in the areas most shadowed by the bars. The barshadow correction is also wavelength-dependent. Figure 4 shows how the barshadow corrections for contiguous microshutters.

The barshadow correction is applied for extended/uniform sources during the Barshadow Correction step (barshadow in calwebb_spec2) using the "BARSHADOW" reference file in CRDS. 

Absolute flux calibration and pixel area correction

ReadTheDocs documentation: Photometric Calibration

Only relevant for extended/uniform sources, the surface brightness is calculated by dividing the measured spectrum by the on-sky area of the given pixels (for slit-like spectrographs, the projected width of the aperture multiplied by the projected cross-dispersion size of the pixel). Due to distortion, the value is a function of location within the field of view and instrument configuration. Note that variations in aperture width (as seen in the fixed slits) are accounted for by the internal flat field correction via S-flat, and no variation in pixel area has been seen as a function of wavelength.

This correction is applied for extended/uniform sources during the Photometric Calibration step (photom in calwebb_spec2) using the "AREA" reference file in CRDS. Note that a single area value per aperture (each MSA shutter, each FS, and each IFU slice) per grating is currently used. 

The aim of the photom step is to apply the flux calibration factor for conversion to physical units, but for NIRSpec, the flux calibration conversion is done in the flat_field step as described earlier in the Section "Flat Fielding". At the photom step, the flux conversion is applied from the reference file, but the value is set to 1.0 for all wavelengths. 

---

Documents for further details

Alves de Oliveira et al., 2022, SPIE, 12180, 3S
In-flight performance and calibration of the grating wheel assembly sensors (NIRSpec/JWST)

Alves de Oliveira, 2018, SPIE, vol 10704, 0Q
Preparing the NIRSpec/JWST science data calibration: from ground testing to sky

Birkmann et al., 2022, A&A, 661, 83
The Near-Infrared Spectrograph (NIRSpec) on the James Webb Space Telescope. IV. Capabilities and predicted performance for exoplanet characterization

Böker et al., 2022, A&A, 661, 82
The Near-Infrared Spectrograph (NIRSpec) on the James Webb Space Telescope. III. Integral-field spectroscopy

Bushouse, H., et al. 2023, Zenodo
JWST Calibration Pipeline

Dorner B. et al. 2016, A&A, 592,113
A model-based approach to the spatial and spectral calibration of NIRSpec onboard JWST

Ferruit et al., 2022, A&A, 661, 81,
The Near-Infrared Spectrograph (NIRSpec) on the James Webb Space Telescope. II. Multi-object spectroscopy (MOS)

Giardino et al., 2022, SPIE, 12180, 0X
Optical throughput and sensitivity of JWST NIRSpec

Giardino et al., 2016, SPIE, vol 9904, 45
The spectral calibration of JWST/NIRSpec: results from the recent cryo-vacuum campaign (ISIM-CV3)

Jakobsen et al., 2022, A&A, 661, 80
The Near-Infrared Spectrograph (NIRSpec) on the James Webb Space Telescope. I. Overview of the instrument and its capabilities

Lützgendorf et al., 2022, SPIE, 12180, 0Y
Astrometric and wavelength calibration of the NIRSpec instrument during commissioning using a model-based approach

Rawle et al., 2016, SPIE, vol 9904, 46
Flat-fielding strategy for the JWST/NIRSpec multi-object spectrograph

---